기초확률이론(Basic Probability Theory)

표본공간(Sample Space) 과 사건(Event)

어떤 시행에서 일어날 수 있는 모든 결과들의 모임을 표본 공간이라고 합니다. 예를 들어 주사위를 한번 던지는 시행의 경우 표본공간은 {1,2,3,4,5,6}와 같은 집합(set)이 됩니다. 그렇다면 이전 시간에 배운 동전던지는 시행을 예로 들어보겠습니다. 앞면과 뒷면이 나올 확률이 0.5로 동일한 동전을 3번 던지는 시행을 한다면 표본공간은 다음과 같이 나타낼 수 있습니다.

$\Omega = \begin{Bmatrix} HHH, HHT,HTH,HTT,THH,THT,TTH,TTT \end{Bmatrix}$ ^{표본공간은 주로 Ω라는 문자로 표현합니다.} $\Omega = \begin{Bmatrix} w_1w_2w_3 : w_i\in \begin{Bmatrix} H,T \end{Bmatrix} for \,\,1 \leq i\leq 3 \end{Bmatrix}$ ^{위의 표본공간을 이렇게도 표현 할 수 있습니다. 학창시절 이런 표현방식을 조건제시법이라고 배웠습니다.}

표본공간 Ω의 부분집합을 사건(Event)라고 합니다. 예를 들어서 위의 표본공간 중에서 처음 동전을 던진 결과가 앞면인 경우는 다음과 같이 표현 할 수 있습니다.

$\begin{Bmatrix} w \in \Omega : w_1=H \end{Bmatrix} = \begin{Bmatrix} HHH,HHT,HTH,HTT \end{Bmatrix}$

확률함수(Probability Function)

우리는 중,고등학교 시절 확률을 배우면서 막연하게 ‘P를 붙이면 확률이 된다.’ 라고 배웠습니다. 이 P는 그냥 붙인다고 확률이 되는 어떤 것이 아니라 수학적으로 함수를 나타냅니다. P라는 함수는 표본공간의 원소를 0과 1사이의 숫자에 대응시키는 함수 입니다. 그렇기 때문에 앞으로 P를 확률함수라고 부르게 될 것입니다(또는 확률측도, probability measure, 라고 부르기도 합니다).

예를 들어서 위의 예제에서 ‘HHH’는 표본공간의 원소입니다. 이 ‘HHH’라는 원소를 1/8이라는 숫자에 대응시키는 것이 확률함수가 하는일 입니다(동전의 앞,뒤가 나올 확률이 1/2로 같기 때문에 앞면이 3번 나올 확률은 1/8입니다). 이를 조금더 우아하게 나타내보면 아래와 같이 표현 할 수 있습니다.

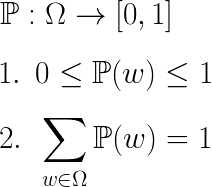
첫 번째 줄은 P라는 녀석이 정의역이 Ω이고 그 원소들을 0과 1사이의 값으로 보내는 함수 라는 뜻 입니다.
두 번째 줄은 보내진 확률 값은 0에서 1사이에 있어야 한다는 뜻 입니다.
마지막 줄은 모든 표본공간의 확률들을 다 더했을 때 그 값은 1이 되어야 한다는 것 입니다.

처음의 예제를 확인해 보면 모든 w에 대해 확률이 1/8이고 확률이 똑같은 것들이 8가지가 있기 때문에 1번과 2번조건을 만족하는 것을 확인 할 수 있습니다. 따라서 ‘동전을 던졌을 때 앞면이 나올 확률이 1/2이고 뒷면이 나올 확률이 1/2’ 라는 확률함수는 표본공간 Ω에 대해 올바르게 정의된 확률함수임을 확인 할 수 있습니다.

이런 확률함수를 이용해서 우리는 위에서 배운 사건에대한 확률도 정의 할 수 있습니다.

$For \: \, A \subseteq \Omega , \:\: \mathbb{P}(A) = \sum_{w \in A}\mathbb{P}(w)$ ^{사건(Event)에 대한 확률은 이렇게 정의 할 수 있습니다.}

예를 들어 위에서 본 처음 동전을 던진 결과가 앞면인 사건에 대해서 확률을 구해보면 다음과 같습니다.

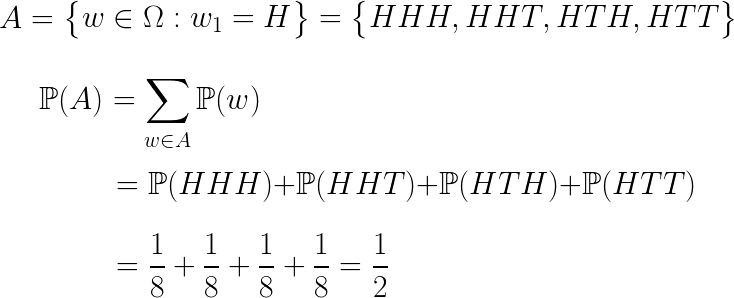
^{처음 동전을 던진 결과가 앞면인 확률은 직관적으로 1/2입니다. 직관과 우리가 정의한 수식이 일치함을 볼 수 있습니다.}

두 사건 A,B가 서로소 라는 것은 사건 A와 B의 교집합이 공집합이라는 뜻 입니다. 그런 경우 아래의 식이 성립합니다. 이는 겹치는 부분이 없기 때문에 직관적으로 받아들일 수 있습니다.

$\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) \:\: when \:\: A \cap B = \varnothing$

확률변수(Random Variables)와 분포(Distribution)

확률변수라 함은 표본공간 Ω에 정의된 실함수를 의미합니다(여기서 실함수는 결괏값이 실수인 함수를 말합니다). 예를 들어 우리가 배웠던 주식가격은 확률변수의 좋은 예제 입니다.

$S_3(HHT) = u^2dS_0, \: S_3(TTT)=d^3S_0 \, ...$ ^{주식가격 S가 Ω의 원소를 어떤 실수값으로 대응시키는 것을 확인 할 수 있습니다.}

주어진 확률변수 X에 대해서 ‘확률함수 P에대한 X의 분포’는 X가 가지는 값에 따라 그 확률을 나열해 놓은 것 입니다. 예를 들어 처음예제의 Ω에서 X를 앞면이 나온 횟수로 정의한다면 X는 0에서 3사이의 값을 가지게 됩니다. 그러면 확률함수 P에 대한 X의 분포는 다음과 같이 적을 수 있습니다.

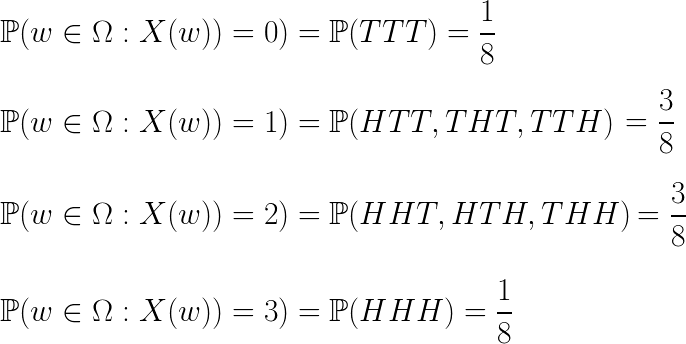
^{확률변수 X의 P에 대한 분포는 이런식으로 X가 가질 수 있는 값들에 대해서 그 확률들을 나열해 주어야 합니다.}

확률변수와 분포의 개념을 혼동하기 쉬운데 둘은 엄연히 다른 개념입니다. 확률변수는 함수입니다. 반면에 분포는 확률변수가 가질 수 있는 값들에대해서 그 확률들을 나열해 놓은 것 입니다.
또 한가지 중요한 점은 어떤 확률변수 X,Y가 확률함수 P에 대해 같은 분포를 가져도 둘은 다른 확률변수일 수 있습니다. 바로 위의 예제에서 Y를 뒷면이 나온 횟수라고 정의한다면 P에 대한 확률분포는 X와 정확히 똑같이 나오게 됩니다. 하지만 분포가 같다고 X와 Y가 같은 확률변수는 아님을 확인 할 수 있습니다.

기대값(Expected Value)

표본공간 Ω에서 정의된 확률변수 X가 있다고 할때 확률함수 P에 대한 X의 기대값은 E[X] 라고 나타내고 다음과 같은 식으로 주어집니다.

$\mathbb{E}[X] = \sum_{w \in \Omega}X(w)\mathbb{P}(w)$

X의 분산은 Var[X]라고 나타내고 다음과 같은 식으로 주어집니다.

$Var[X] = \mathbb{E}[(X-\mathbb{E}(X))^2]$ ^{분산의 정의 입니다.} $Var[X] = \mathbb{E}[X^2]-(\mathbb{E}[X])^2$ ^{실제 계산은 변형된 이 식을 더 많이 사용합니다.}

분산의 정의는 위의 식이지만 실제 계산에서는 아래의 식을 더 선호합니다. 두 식은 똑같은 값이 나오는데 증명은 위키피디아 링크를 걸어 두도록 하겠습니다.

기대값의 선형성

기대값은 선형성(linearity)이라는 성질을 가지고 있습니다. 수학에서 선형성에 대한 정의는 다음과 같습니다.

함수 f에 대해,
1.임의의 수 x,y에 대해 f(x+y) = f(x) + f(y) 가 항상 성립하고
2.임의의 수 x와 a에 대해 f(ax)=af(x) 가 항상 성립할 때
함수 f는 선형이라고 합니다.

따라서 확률변수 X,Y와 임의의 실수 a,b에 대해서 다음 식이 성립하게 됩니다. 증명은 기대값의 정의를 풀어서 써 보시면 시그마(summation)기호가 선형성을 가지기 때문에 쉽게 유도가 가능합니다.

$\mathbb{E}[aX+bY] = a\mathbb{E}[X] + b\mathbb{E}[Y]$

특히 선형함수인 L(x)에 대해서 다음 식이 성립하게 됩니다. 아래의 위의 방식과 똑같이 증명 할 수 있습니다.

$\mathbb{E}[L(X)] = L(\mathbb{E}[X])$ ^{선형인 함수 L에 대해서만 기대값 과의 계산 순서를 바꿀 수 있습니다.}